チャレンジ問題【パート3】
問題
[1]
1辺の長さが\(a\)である正四面体\(A\)について, \(A\)の各辺 (6つの辺すべて)に接する半径\(R_0\)を求めよ。
[2]
1から8までの番号が書かれたカードが1枚ずつある。これらのカードを区別のつかない3つの袋に分けて入れる
(1)
1枚もカードが入らない袋があってもよいものとするとき, 分け方は全部で何通りあるか。
(2)
どの袋にも1枚以上のカードが入っているような分け方は全部で何通りあるか。
[3]
\(a, b, c\)はいずれも2以上の整数で, \(a<=b<=c\)であるとする。\(abc=2a+3b+7c-3\)が成り立つような\(a, b, c\)の組をすべて求めよ。
解答
[1]
一般的に, 立方体に対し右図のように4点\(A, B, C, D\)をとって結ぶと正四面体ができる。(図1)
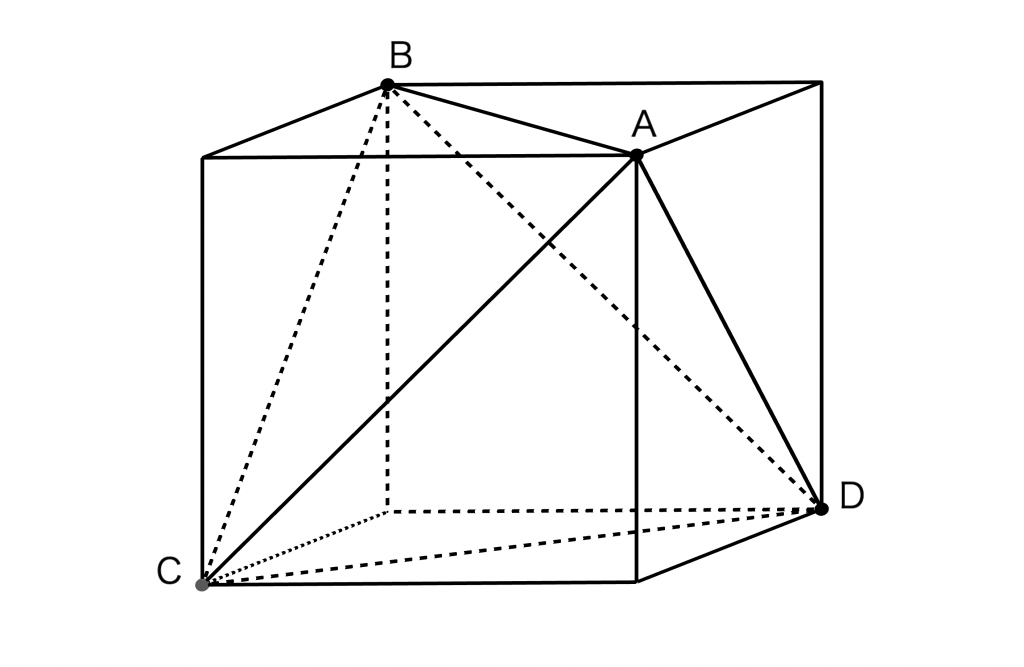
すなわち, 任意の正四面体に対し, 必ず立方体を外接させることができる。
正四面体\(A\)に対して, 立方体を概説させたときの立方体の1辺の長さを\(L\)とすると,
\(\sqrt{2}L=a\) ∴\(L=\frac{a}{\sqrt{2}}\)
ここで, この立方体にな内接する球\(S\)を考えた時, 球\(S\)は正四面体\(A\)の6つの辺すべてに接している (接点は正四面体\(A\)の6つの辺の中点, すなわち立方体の6つの面の中心) (図2)
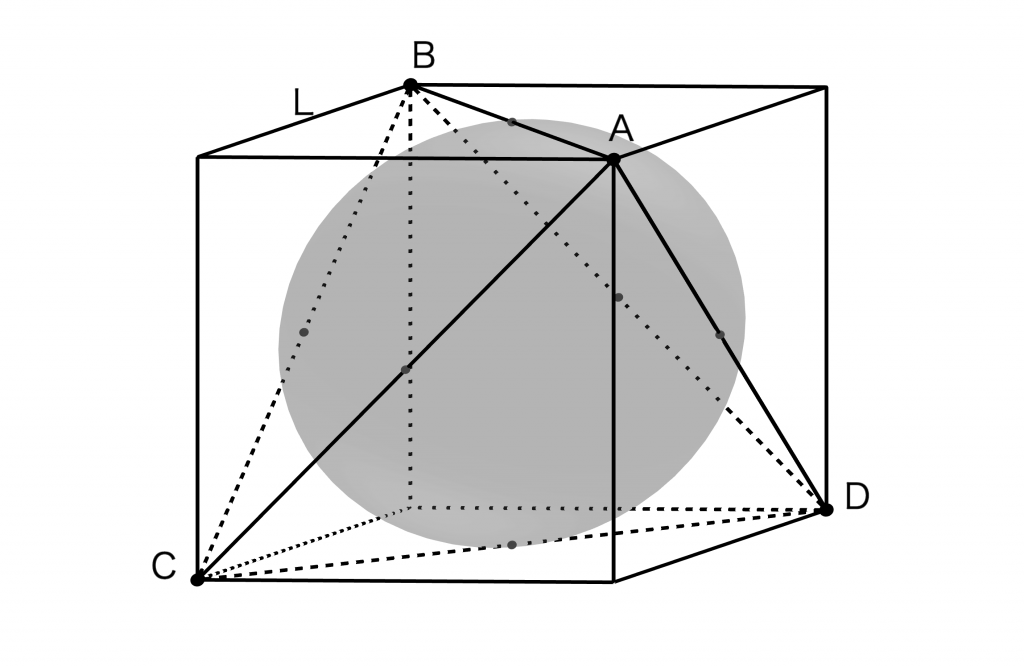
球\(S\)の直径は立方体の1辺の長さ\(L\)であるから, 求める半径\(R_0\)は
\(R_0=\frac{1}{2}L=\frac{a}{2\sqrt{2}}=\frac{\sqrt{2}}{4}a\) ・・・(答)
[2]
方針
まず初めに組に区別をつけて考えた後で区別をなくし”重複”を除く
(1)
3つの袋を\(A, B, C\)と区別して考える。1枚もカードが入らない袋があっても良い場合は, カードの分け方は全部で
\(3^8=6561\) (通り)
(i) 8枚のカードを1つの袋だけに入れる分け方は\(3\) (通り)
(ii) 1枚もカードが入らない袋が1つ以下となるような分け方は\(3^8-3=6558\) (通り)
ここで袋の区別をなくすと, (i)には\(3\)通り, (ii)には\(3!=6\)通りずつ同じ分け方が含まれる。
∴求める分け方の総数は
\(\frac{3}{3}+\frac{3^8-1}{3!}=1+1093=1094\) (通り) ・・・(答)
(2)3つの袋に\(A, B, C\)と区別があるもとで, どの袋にも少なくとも1枚のカードが入っているような分け方は
\(3^8-{3+3(2^8-2)}=6561-(3+3\cdot254)=5796\) (通り)
1つの袋だけが空となる分け方について, 空の袋の選び方が \({}_3 C_1=3\) (通り)で, 残りの2つの袋には少なくとも1枚のカードが入ることから, \(3(2^8-2)\) (通り)
ここで袋の区別をなくすと, \(3!=6\) (通り)ずつの重複を考えればよいから, 求める分け方は
\(\frac{5796}{3!}=966\) (通り)
[3]
方針
不等式変形により解の候補の絞り込みを行う
(1)
\((2<=)a<=b<=c\)を用いて不等式を変形していくと,
\begin{eqnarray}abc&=&2a+3b+7c-3<2a+3b+7c\\&<=&2c+3c+7c=12c\\ ∴abc&=&12c\end{eqnarray}
が成り立つ。
ここで \(c>=2>0\) であるから,
\(abc<12c\Rightarrow ab<12\)
また, \(2<=a<=b\) より \(4<=ab\)
したがって \(4<=ab<12\)
∴\((a,b)=(1,2),(2,3),(2,4),(2,5),(3,3)\)
に絞り込める。
この5組各々に対し, 与式から直接\(c\)の値を求めると \(c=-\frac{7}{3},-10,13,\frac{16}{3},6\)
以上の組のうち, \(a,b,c\) がいずれも2以上の整数かつ \(a<=b<=c\) を満たす組は \((a,b,c)=(2,4,13),(3,3,6)\)・・・(答) のみで, これが求める組である。

